機械安全の「ブラックボックス」を開く：ISO/CD TR 13849-3に基づくマルコフモデルPFH計算の詳細解説

みなさんこんにちは。こんばんは。ジュンイチロウです。

技術の進化と共に、私たちを取り巻く規格も日々アップデートされています。特に、機械の安全設計に携わる皆様にとっては、最新規格のキャッチアップが欠かせない業務の一つではないでしょうか。

そんな目まぐるしく変化する規格の世界で、今、注目すべき新たな動きがあります。それは、機械の制御システムの安全関連部に関する重要規格「ISO 13849」シリーズに、新たな技術報告書（TR）「ISO/TR 13849-3」の発行が予定されているというニュースです。

「ただでさえ複雑なISO 13849に、また新しい考え方が加わるのか…」と驚かれた方もいらっしゃるかもしれません。

この記事では、正式発行を前に、この「ISO/TR 13849-3」がどのような内容になる可能性があるのか、そしてなぜ私たちが今から注目すべきなのかを、分かりやすく解説していきます。

第1部：なぜ今、PFH計算の「ブラックボックス」を開く必要があるのか？

1．はじめに：機械安全の新たな章の幕開け

新しいISO 13849-3 （機械の安全性-制御システムの安全関連部　パート3:マルコフモデルに基づくPFH計算）は、機能安全評価の世界における極めて重要な変化を解説するためのガイドです。私たちがこれから探求するのは、近日発行が予定されている技術報告書ISO/TR 13849-3の核心、すなわちマルコフモデルを用いた先進的な信頼性評価手法です。

これは単なる規格のマイナーアップデートではありません。長年、多くの設計者にとって「ブラックボックス」であったPFH（時間当たりの危険側故障の平均確率）計算の根拠を明らかにし、私たち技術者に透明性と強力な分析ツールをもたらす、まさにパラダイムシフトと言えるものです。

本シリーズを通じて、この先進的な手法の理論的背景から実践的な応用までを、段階的に、そして深く掘り下げていきます。まずは、なぜ今、この「ブラックボックス」を開くことが不可欠なのか、その背景から見ていきましょう。

2.1 安全評価の進化：ルールから確率へ

機械の制御システムの安全設計は、ISO 13849規格群によって体系化されています 。この規格は、安全機能を提供する制御システムの一部、すなわち「制御システムの安全関連部（SRP/CS）」の設計原則を定めたISO 13849-1と、その妥当性評価（バリデーション）を規定したISO 13849-2から構成されています 。

安全設計のプロセスは、反復的なアプローチが基本です。まず、ISO 12100に基づき機械に潜むハザードを特定するリスクアセスメントを行います 。次に、特定されたハザードごとに、傷害のひどさ（S）、暴露の頻度（F）、回避の可能性（P）という3つのパラメータを用いてリスクを見積もり、そのリスクを十分に低減するために必要となるパフォーマンスレベル（PLr）を決定します 。そして最後に、設計者はこのPLrを達成するSRP/CSを設計し、その性能を検証・妥当性評価するのです 。

ISO 13849がもたらした最も重要な変化は、旧規格EN 954-1が主としていた、故障に対する耐性といった構造的なアプローチから、確率論的なアプローチへと移行した点にあります 。この確率論的アプローチの中心となる指標が、PFH（時間当たりの危険側故障の平均確率）です。PFHは、SRP/CSが1時間あたりに危険な故障を起こす確率を定量的に示したものであり、パフォーマンスレベル（PL aからeまでの5段階）は、このPFH値の特定の範囲に対応付けられています 。この移行により、安全性能を客観的かつ定量的に評価し、議論することが可能になったのです。

2.2 「簡略化手法」：便利なツールが持つ、見過ごせない限界

ISO 13849-1は、設計者がSRP/CSのPLを評価するために、4つの主要なパラメータを導入しました。

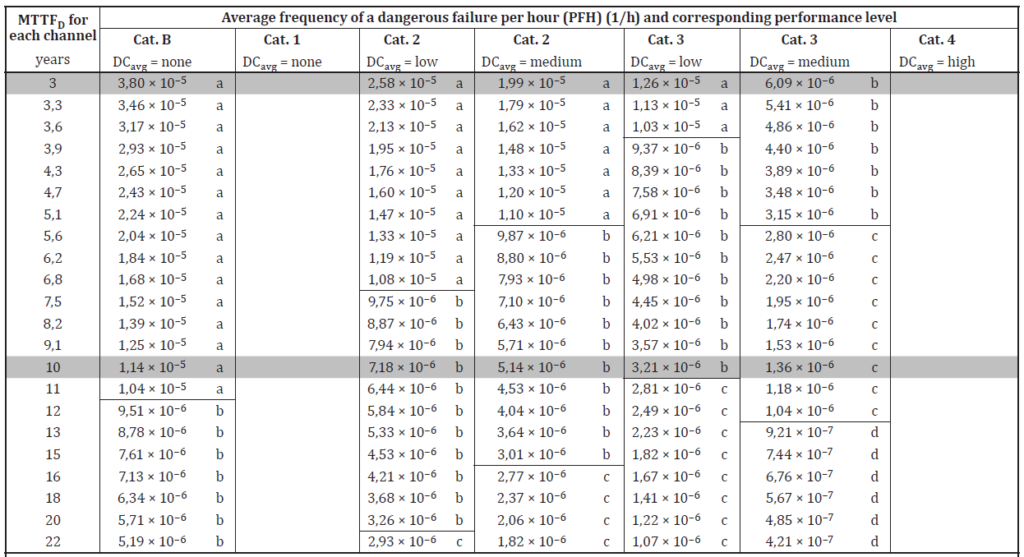
ISO 13849-1 は、これらのパラメータからPLを導き出すための「簡略化手法」を提供しています。具体的には、規格の図12に示されるグラフや、附属書Kの表に記載されたPFH値を用いることで、設計者は比較的容易にPLを評価できます 。この手法は、特に一般的な構成のSRP/CSに対して、迅速かつ簡便に評価を行えるという大きな利点があり、広く普及してきました。

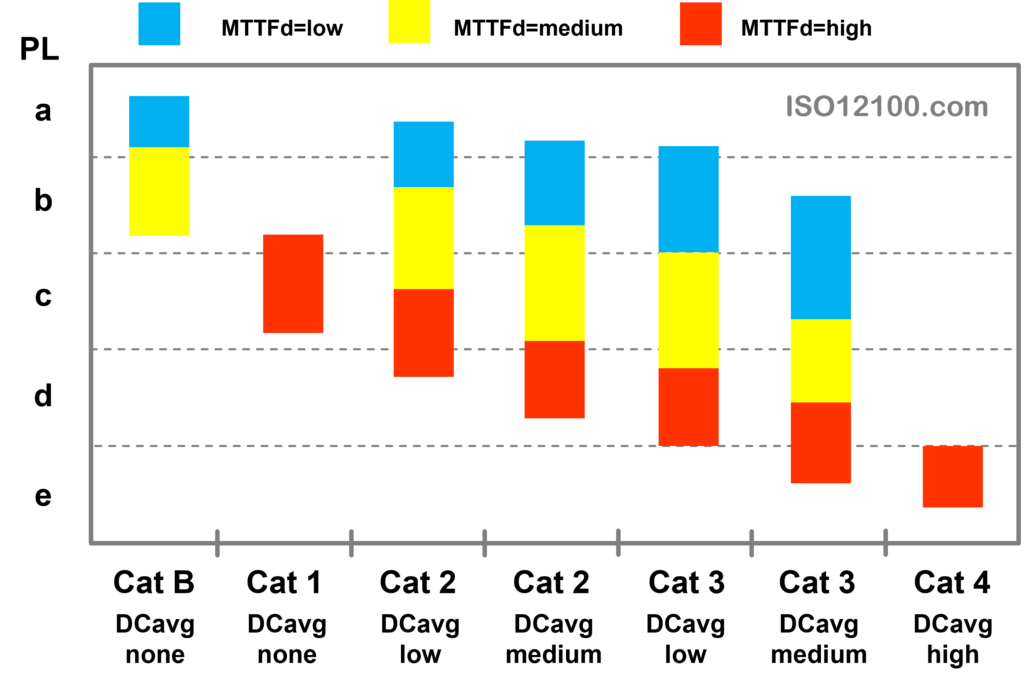
しかし、この便利さの裏には、本質的な限界が存在します。最大の問題は、附属書Kの表に示されたPFH値が、非公開のマルコフモデルに基づいて事前計算された結果であるという点です 。これにより、設計者は計算の根拠となる前提条件（例えば、共通原因故障のβファクタの具体的な値や、診断チャネルの故障率の仮定など）を知ることができず、計算プロセスは完全に「ブラックボックス」化されています。その結果、設計者は計算結果を独自に検証することも、規格で想定されていない非標準的なアーキテクチャや特殊な条件下でのPFHを正確に計算することもできませんでした。

2.3 透明性の夜明け：ISO/TR 13849-3が果たす役割

このような背景から、新たな技術報告書（TR）であるISO/TR 13849-3の策定が進められています。この文書は現在、委員会原案（CD）から国際規格案（DIS）へと進展しており、その発行が待たれています 。その最大の目的は、これまで非公開であった、附属書KのPFH値の算出根拠となったマルコフモデルを公開し、その適用方法を詳細に解説することにあります 。

この透明性の確保は、現代の複雑なシステムを扱う上で、もはや不可欠です。なぜなら、簡略化手法では対応できないシナリオが増えているからです。例えば、複数のハザードが重畳する複雑なシステム 、ソフトウェアによる高度な診断機能を持つシステム、あるいは従来の指定アーキテクチャには当てはまらない独自の構成を持つシステムなどです 。これらのシステムを正しく評価するには、簡略化手法の前提条件から逸脱した、現実に即したモデルを構築する必要があります。

この動きは、単に技術的な詳細が公開される以上の意味を持っています。それは、安全技術者に求められる能力の質的な変化を示唆しています。これまで、規格の利用者は、附属書Kの表を参照するだけでした。しかし、ISO/TR 13849-3の登場により、これからは計算の基礎となる数学モデルを理解し、適用できる「信頼性工学の実践者」であることが求められるようになります。これは、業界が簡便な「クックブック」的なアプローチから脱却し、より広範な機能安全規格であるIEC 61508の精神に近い、工学的で深い信頼性理解へと向かっていることの現れです 。

さらに、この変化は法的な意味合いも持ちます。ISOによって、より正確で透明性の高い評価手法が公式に提示されれば、それが新たな「技術最高水準（state of the art）」と見なされるようになる可能性があります。特に、PLdやPLeといった高い安全性が要求される複雑なシステムにおいて、簡略化手法を使い続けることの正当性を説明するのは、将来的に困難になるかもしれません。万が一の事故の際、なぜより厳密な評価手法を用いなかったのかが問われる可能性があるのです。これは、企業の設計プロセス、文書化、そしてリスクマネジメントに大きな影響を与える、避けては通れない変化なのです。

第2部：PFH計算のエンジン「マルコフモデル」入門

3.1 状態と遷移で考える：マルコフモデルの中心概念

前部では、PFH計算の「ブラックボックス」を開く必要性についてお話ししました。この部では、そのブラックボックスの中身、すなわち「マルコフモデル」の基本的な考え方を解説します。難解に聞こえるかもしれませんが、その中心概念は非常に直感的です。

マルコフモデルは、システムの振る舞いを「状態」と「遷移」という2つの要素で捉えるアプローチです 。これを理解するために、信号機を例に考えてみましょう。

このように、複雑なシステムの振る舞いを、有限個の状態とそれらの間の遷移というシンプルなモデルに落とし込むのが、マルコフ解析の第一歩です。

3.2 「無記憶性」という重要な仮定

マルコフモデルを成り立たせている、最も重要な数学的な仮定が「無記憶性（Memoryless Property）」です 。

これは、「システムが将来どの状態に遷移するかの確率は、現在の状態のみに依存し、過去にどのような経緯でその状態に至ったかには依存しない」という性質を指します。

再び信号機の例で言えば、今「青」である信号機が次に「黄」になる確率は、その信号機が10秒前に青になったのか、あるいは30秒前に青になったのかには関係しない、ということです。この無記憶性は、数学的には、故障や修復といった事象の発生時間間隔が「指数分布」に従うという仮定によって表現されます。この仮定により、複雑な確率過程を、比較的扱いやすい数学モデルで解析することが可能になるのです。

3.3 変化を数値化する：故障率（λ）と修復率（μ）

状態遷移図が描けたら、次はその変化の「速さ」を数値で定義します。ここで登場するのが、故障率と修復率です。

これらの率を状態遷移図の各矢印に割り当てることで、システムの動的な振る舞いを定量的にモデル化する準備が整います。

3.4 図から予測へ：モデルの背後にある数学

状態遷移図と各遷移率が定義されると、それらは「チャップマン・コルモゴロフの微分方程式」として知られる連立微分方程式に変換されます 。

ある状態 i の確率 Pi​(t) の時間変化率 dPi​(t)/dt は、「他の全ての状態 j から状態 i への確率の流入率の合計」から、「状態 i から他の全ての状態 j への確率の流出率の合計」を引いたものとして、以下のように表されます。

$$\frac{ dP_{i}​(t) }{ dt }​= \displaystyle \sum_{j \neq i}P_{j}​(t)λ_{ji}​−P_{i​}(t)\displaystyle \sum_{j \neq i}λ_{ij}$$

ここで、λji​ は状態 j から状態 i への遷移率です。

機能安全の文脈で特に重要なのは、システムが十分に時間が経過した後の「定常状態」です。定常状態では、各状態の確率は時間的に変化しなくなるため、dPi​(t)/dt=0 となります。これにより、上記の微分方程式は連立の代数方程式となり、これを解くことで各状態に存在する定常確率 Pi​ を求めることができます 。

最終的な目標である PFH は、システムが安全な状態（危険な故障が発生していない状態）から、危険な状態（ハザードにつながる故障状態）へ遷移する頻度の総和として計算されます。具体的には、全ての安全な状態 i について、「その状態にいる確率 Pi​」と「その状態から危険な状態へ遷移する率 λi,hazardous​」の積を求め、それらを全て足し合わせることで算出されるのです 。

$$PFH= \displaystyle \sum_{i \in SafeStates}P_{i​}×λ_{i,hazardous​}$$

このように、マルコフモデルは、システムの振る舞いを視覚的な図から厳密な数学方程式へと変換し、PFHという具体的な安全指標を導出するための強力なエンジンとなるのです。

次の部からは、この理論をISO 13849-1の具体的なパラメータと結びつけていきます。そのために、まずはここで登場した重要な用語を一覧で確認しておきましょう。

用語・記号	定義
状態 (State)	システムがとりうる特定の離散的な状況（例：正常、故障）
遷移 (Transition)	システムがある状態から別の状態へ変化すること
λ (故障率)	コンポーネントが単位時間あたりに故障する率。MTTFの逆数に近似されます。
μ (修復率)	故障したコンポーネントが単位時間あたりに修復される率。MTTRの逆数。
Pi​(t) (状態確率)	時刻 t において、システムが状態 i にある確率。
Q (遷移率行列)	状態間の遷移率 λij​ を要素とする行列。システムの動特性を記述します。
PFH	時間当たりの危険側故障の平均確率 (Average Probability of Dangerous Failure per Hour)。安全状態から危険状態への遷移率の総和として計算されます。
MTTFd	危険側故障までの平均時間 (Mean Time to Dangerous Failure)。
DC	診断範囲 (Diagnostic Coverage)。危険側故障のうち、診断によって検出される割合。
CCF	共通原因故障 (Common Cause Failure)。単一の原因で複数の冗長チャネルが同時に故障すること。
β (βファクタ)	共通原因故障の発生しやすさを示す係数。

第3部：ISO 13849-1のパラメータをマルコフモデル言語に翻訳する

はじめに：理論と実践をつなぐ「翻訳」作業

前部では、マルコフモデルの基本的な理論について学びました。しかし、この理論を実際の安全設計に役立てるためには、私たちが普段使っているISO 13849-1のパラメータ（MTTFd, DC, CCFなど）を、マルコフモデルの「言語」、すなわち遷移率に「翻訳」する必要があります。この部は、その翻訳作業を行うための解説です。

4.1 MTTFdから故障率（λD​）へ

最も直接的な翻訳は、コンポーネントの基本的な信頼性を示すMTTFd（危険側故障までの平均時間）です。マルコフモデルにおいて、これは危険側故障率 λD​ に変換されます。MTTFdが時間単位で与えられている場合、その逆数が故障率となります 。

$$ {λ_{D}}​≈\frac{1}{MTTF_{d}}​​$$

この λD​ は、モデル内でシステムが「正常（OK）」状態から「危険側故障」状態へ遷移する際の、基本的な遷移率として用いられます。

4.2 診断範囲（DC）のモデリング：運命の分かれ道

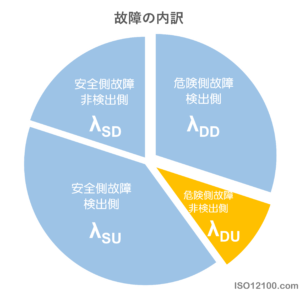
DC（診断範囲）は、発生した危険側故障のうち、診断機能によってどれだけ検出できるかを示す割合です。これはマルコフモデルにおいて非常に巧みに表現されます。故障による遷移を、一本道ではなく「運命の分かれ道」として、二つに分岐させるのです。

あるチャネルが危険側故障率 λD​ で故障する場合、単一の「故障状態」へ遷移するのではなく、以下の二つの異なる状態へ、それぞれの確率で遷移するものとしてモデル化します 。

• 危険側検出（Dangerous Detected, DD）状態への道: 診断機能によって故障が検出された場合の経路です。この状態への遷移率は、元の故障率にDCを乗じたものになります。
  
  $$λ_{DD}​=λ_{D}​×DC$$
• 危険側未検出（Dangerous Undetected, DU）状態への道: 診断機能が見逃してしまった場合の経路です。この状態への遷移率は、元の故障率に「1 – DC」を乗じたものになります。
  
  $$λ_{DU}​=λ_{D}​×(1−DC)$$

この「遷移の分岐」モデリングは、診断機能の有効性を確率論的にモデルへ組み込むための基本であり、特にカテゴリ2、3、4のような診断機能を持つアーキテクチャを解析する上で不可欠な手法です。

4.3 共通原因故障（CCF）のモデリング：冗長性のアキレス腱

CCF（共通原因故障）は、冗長アーキテクチャ（カテゴリ3、4）の信頼性を評価する上で、最も重要な要因です。これは、過電圧や極端な温度、ソフトウェアのバグといった単一の事象が、独立しているはずの複数の冗長チャネルを同時に機能不全に陥らせる現象を指します。

マルコフモデルでは、CCFはシステムの信頼性における「近道（ショートカット）」として表現されます。つまり、「全チャネル正常（OK）」状態から、中間的な単一チャネル故障状態を経由せず、「全チャネルが危険側故障した状態（ハザード状態）」へ直接遷移するパスとしてモデル化されるのです。

この直接遷移の率は、IEC 61508などで用いられるβファクタモデルに基づいて計算されます 。βファクタは、あるコンポーネントの故障のうち、共通原因によって引き起こされる故障の割合を示します。例えば、βが2%（0.02）の場合、全故障の2%がCCFに起因すると仮定されます。CCFによる遷移率 λCCF​ は以下のようにモデル化されます 。

$$λ_{CCF}​=β×λ_{D,equivalent}​$$

ここで、λD,equivalent​ は共通原因の影響を受ける冗長コンポーネントの等価的な危険側故障率です。この遷移パスをモデルに組み込むことで、冗長性による信頼性向上の効果が、CCFによってどの程度相殺されてしまうのかを定量的に評価できます。

この翻訳作業は、設計上の選択がPFHにどう影響するかを可視化する強力な手段です。例えば、設計者はより高性能な診断コンポーネントに投資してDCを向上させる（λDU​ を減少させる）ことも、あるいは物理的な分離を徹底してβファクタを低減させる（λCCF​ を減少させる）こともできます。以前はこれらの選択の影響を附属書Kの離散的な値でしか評価できませんでしたが、マルコフモデルを使えば、「DCを90%から95%に向上させること」と「βを2%から1%に低減させること」が、最終的なPFHにどれだけの改善をもたらすかを正確に比較検討できます。これにより、安全性、コスト、性能のバランスを、データに基づいて最適化する、真のエンジニアリングが可能になるのです。モデルは単なる検証ツールから、優れた設計を生み出すためのデザインツールへと進化します。

4.4 テスト率とデマンド率（rt​, rd​）のモデリング：カテゴリ2の動特性

特定のアーキテクチャ、特にカテゴリ2においては、システムの安全性がテストの頻度と安全機能が要求される頻度に依存します。これらも遷移率としてモデル化されます。

これらのパラメータを遷移率としてモデルに組み込むことで、ISO 13849-1の各アーキテクチャを数学的に解析する準備が整いました。次の部では、いよいよこれらのツールを使って、指定アーキテクチャのPFHを導出していきます。

第4部：実践編：指定アーキテクチャのPFHを導出する

はじめに：理論から具体的な数値へ

これまでの部で、マルコフモデルの理論と、ISO 13849-1のパラメータをモデルの言語に翻訳する方法を学びました。この部では、いよいよそれらの知識を総動員し、ISO 13849-1で定義されている主要な指定アーキテクチャ（カテゴリ2, 3, 4）のPFHを実際に導出するプロセスを見ていきましょう。各アーキテクチャについて、「アーキテクチャの記述」「状態遷移モデル」「PFHの計算」という3つのステップで体系的に解説します。

5.1 ケーススタディ：カテゴリ2（単一チャネル・診断付きシステム）

5.1.1 アーキテクチャの記述

カテゴリ2は、単一の機能チャネル（F）と、それを監視する独立したテスト機器（TE）またはモニタリングチャネル（M）で構成されるアーキテクチャです 。この構成の弱点は、機能チャネルに危険側故障が発生してから、次のテストでそれが検出されるまでの間は、安全機能が失われる可能性があるという点です。したがって、その安全性はテストの頻度と有効性（診断範囲）に大きく依存します。

5.1.2 状態遷移モデルと状態定義

カテゴリ2のSRP/CSは、以下の主要な状態を持つマルコフモデルで表現できます。

状態ID	状態名	状態の説明	状態の説明
S1	OK	機能チャネル(F)とモニタリングチャネル(M)の両方が正常に動作している。	安全
S2	F_DU	Fに未検出の危険側故障が発生している。Mは正常。	危険（潜在的）
S3	F_DD	Fの危険側故障がMによって検出された。システムは安全な状態に移行する。	安全（劣化）
S4	M_D	Mに危険側故障が発生している。Fは正常。	危険（潜在的）
S5	F_DU + M_D	Fに未検出の危険側故障があり、かつMも故障している。	危険
S6	HAZ	ハザード事象発生。F_DU状態でデマンドが発生した場合など。	ハザード

これらの状態間の遷移は、前部で定義した遷移率によって決まります。例えば、状態S1（OK）から状態S2（F_DU）への遷移率は、機能チャネルの未検出危険側故障率 λDU,F​ です。そして、この危険な潜在状態S2から、テストによって安全な状態S3へ移行する遷移率がテスト率 rt​ であり、デマンドの発生によってハザード状態S6へ移行する遷移率がデマンド率 rd​ となります 。

5.1.3 PFHの計算

この状態遷移モデルから導出されるPFHの近似式は、非常に示唆に富んでいます 。

$$PFH_{Cat2}\approx λ_{DU,F}\frac{​T_{d}}{T_{t}}​​+λ_{D,M}​$$

この式は、カテゴリ2のPFHが主に2つの要素で決まることを物語っています。第1項は「機能チャネルの未検出故障率（λDU,F​）と、デマンド率とテスト率の比（rd​/rt​）の積」です。これは、未検出の故障が存在する状態でデマンドが発生するリスクを表しており、いわば「デマンドが到着する(rd​)のと、テストが故障を発見する(rt​)のとの競争」で、デマンドが勝ってしまう確率を示しています。第2項は「モニタリングチャネル自体の故障率（λD,M​）」です。この式から、テスト頻度を高くすること（rt​ を大きくする）が、PFHを低減させる上でいかに重要であるかが定量的に理解できます。

5.2 ケーススタディ：カテゴリ3（冗長・相互監視システム）

5.2.1 アーキテクチャの記述

カテゴリ3は、2つの冗長なチャネルが互いに相互監視（クロスモニタリング）を行うアーキテクチャです 。この構成の強みは、いずれか一方のチャネルに単一の故障が発生しても、もう一方のチャネルが安全機能を維持するため、直ちに安全機能が失われることはない点です。しかし、最初の故障が検出されないまま放置され、その後に2番目のチャネルも故障すると安全機能が失われる（故障の累積）、あるいは共通原因故障（CCF）が発生するという脆弱性を持っています。

5.2.2 状態遷移モデルと状態定義

カテゴリ3のマルコフモデルは、カテゴリ2よりも複雑になりますが、主要な状態は以下の通りです。

状態ID	状態名	状態の説明	状態の説明
S1	OK	両方のチャネルが正常に動作している。	安全
S2	1ch_F_DU	一方のチャネルに未検出の危険側故障が発生している。もう一方は正常。	安全（劣化）
S3	1ch_F_DD	一方のチャネルの危険側故障が他方のチャネルによって検出された。	安全（劣化）
S4	HAZ	ハザード事象発生。CCFの発生、または1ch_F_DU状態で他方のチャネルが故障した場合。	ハザード

状態S1（OK）からは、主に3つの経路で故障状態へ遷移します。一つは、両チャネルが共通原因故障で同時に故障する経路（遷移率 λCCF​=βλD​）。もう一つは、片方のチャネルが独立して故障し、それが検出されない経路（遷移率 2λDU​）。そして、片方のチャネルが独立して故障し、それが検出される経路（遷移率 2λDD​）です。ハザード状態（S4）へは、S1からのCCFによる直接遷移、またはS2（1ch_F_DU）状態から残りの正常なチャネルが故障する（遷移率 λD​）ことによって到達します 。

5.2.3 PFHの計算

このモデルから導出されるPFHの近似式は、カテゴリ3の弱点を明確に示しています。

$$PFH_{Cat3}​ \approxβ\cdot (2λ_{D}​)+(2λ_{DU}​)^{2}\cdot T_{mission​}$$

ここで、Tmission​ はシステムのミッション時間（通常20年）です。この式は、カテゴリ3の主な敵が二つあることを教えてくれます。第1項は「共通原因故障（CCF）」という、冗長性を根底から覆す外部からの攻撃です。第2項は「二つの独立した未検出故障の累積」という、内部に潜む見えない脅威です。通常、λD​ は非常に小さいため、2乗の項は無視できるほど小さくなります。したがって、カテゴリ3のPFHは、実質的にCCFの発生率（βファクタ）によって支配されることが多く、冗長システムの設計においてCCF対策（Annex Fのスコア65点以上など）がいかに重要であるかを数学的に物語っています。

5.3 ケーススタディ：カテゴリ4（高信頼性冗長システム）

5.3.1 アーキテクチャの記述

カテゴリ4は、カテゴリ3をさらに強化した、最高の信頼性を持つアーキテクチャです。基本的な冗長構造は同じですが、診断範囲が「高」（DCavg ≥ 99%）であることが要求されます 。これにより、単一の故障は次のデマンドまでにほぼ確実に検出され、未検出故障の累積が安全機能の喪失につながるリスクを限りなくゼロに近づけます。

5.3.2 モデリングアプローチ

カテゴリ4のマルコフモデルは、構造的にはカテゴリ3と全く同じです。しかし、遷移率の大きさが決定的に異なります。DCが99%以上であるため、未検出の危険側故障率 λDU​=λD​×(1−DC) は極めて小さくなります。これにより、状態S2（1ch_F_DU）へ遷移する確率が大幅に低下します。

5.3.3 PFHの計算

カテゴリ4のPFH計算式は、カテゴリ3の式と同じ形式で表されます。

$$PFH_{Cat4}\approx β\cdot (2λ_{D}​)+(negligibly\ small\ term)$$

$$PFH_{Cat4}\approx β\cdot (2λ_{D}​)$$

しかし、λDU​ の値が非常に小さいため、二重故障の累積による第2項の寄与は事実上無視できるほど小さくなります。結果として、カテゴリ4のPFHは、ほぼ完全にCCFの項によって決定されます。これは、優れた診断機能によって「内部の脅威（独立故障の累積）」をほぼ排除した結果、残る主要な敵は「外部からの攻撃（CCF）」だけになる、ということを示しています。これが、カテゴリ4が最高のパフォーマンスレベルであるPLeを達成できる根拠であり、設計においてCCF対策の徹底が最優先課題となる理由なのです。

第5部：簡略化手法の限界を超えて

6.1 実践テスト：附属書Kの値を再現する

ISO/TR 13849-3がもたらす透明性の価値を具体的に示すため、ISO 13849-1の附属書Kに記載されたPFH値が、マルコフモデルを用いてどのように導出されるかを検証してみましょう。ここでは、一般的なシナリオとしてカテゴリ3のSRP/CSを想定します。

計算プロセス:

1. 簡略化手法（附属書K）による参照:
   ISO 13849-1:2023の表K.1を参照すると、カテゴリ3、MTTFd=High、DCavg=Mediumの組み合わせに対応するPFH値は 4.29×10^-8 [1/h] とします 。
2. マルコフモデルによる計算:
   第4部で導出したカテゴリ3のPFH近似式と、上記前提条件を用いて計算します。

• 各チャネルの危険側故障率:
  $$λ_{D}​=\frac{1}{100年×8760時間/年}\quad \approx 1.14×10^{-6}\quad [1/h]$$
• 未検出危険側故障率:
  $$λ_{DU}​=λ{D}​×(1−DC)=1.14×10^{-6}×(1−0.90)=1.14×10^{-7} \quad [1/h]$$
• PFHの計算:
  
  $$PFH_{Cat3}\approx β⋅(2_λ{D}+(2λ_{DU}​)^{2}⋅T_{mission}​$$
  
  $$ PFH_{Cat3} \approx (0.02 \cdot 2 \cdot 1.14 \times 10^{-6}) + (2 \cdot 1.14 \times 10^{-7})^2 \cdot (20 \times 8760) $$
  $$ PFH_{Cat3} \approx 4.56 \times 10^{-8} + 9.13 \times 10^{-9} \approx 5.47 \times 10^{-8} \text{ [1/h]} $$

附属書Kの値と計算結果に差異がありますが、これは附属書Kが修復状態などを含むより詳細なモデルを解いた結果であるためです 。しかし重要なのは、PFHのオーダー（桁数）と、その主要な寄与因子（CCFと二重故障）を理論的に把握できる点です。そして、もし設計者がこれらの前提条件（例えばβ=2%）を変更できる正当な理由を持つならば、より現実に即したPFH値をマルコフモデルによって算出できることがわかります。

6.2 「クックブック」が機能しないとき：マルコフ解析が不可欠なシナリオ

附属書Kに頼る簡略化手法は、多くの標準的なケースで有効ですが、その適用範囲を超えた途端、不正確または不適切な結果を導く可能性があります。以下に、完全なマルコフ解析が不可欠となるシナリオを挙げます。

これらのシナリオは、技術の進歩とともにますます一般的になっています。マルコフモデルの活用は、設計者に「規格のカテゴリに設計を合わせる」という制約から、「最適なシステムを設計し、その安全性をモデルで証明する」という自由をもたらします。かつてエンジニアは、たとえ別の構成が効率的であっても、自らの設計をカテゴリ2、3、4という既定の箱に無理やり押し込めなければならないと感じることがありました。マルコフモデルは、その制約から設計者を解放します。革新的なアーキテクチャを自由に考案し、その故障挙動をモデル化してPFHが要求PLを満たすことを証明できれば、その設計は正当なものとして認められるのです。これは、単なる規格遵守ではなく、真の技術革新を促進する大きな一歩です。

この価値をより明確にするために、以下の比較表をご覧ください。

前提条件	PFH (附属書K) [1/h]	PFH (マルコフモデル計算) [1/h]	パフォーマンスレベル (PL)	解説
ベースライン (β=2%, DC=90%, MTTFd=100年)	2.06×10^-7	≈5.47×10^8	d (附属書K) / e (モデル)	附属書Kは保守的な値を含む可能性があります。モデル計算ではPL eの範囲に入ります。
CCF対策強化 (β=1%に改善)	2.06×10^-7	≈3.19×10^8	d (附属書K) / e (モデル)	簡略化手法ではCCF対策強化の効果を反映できませんが、マルコフモデルではPFH値の明確な改善が示されます。
非対称チャネル (MTTFd1=100年, MTTFd2=40年)	適用不可	≈7.00×10^8	適用不可 / e (モデル)	簡略化手法は非対称な構成を想定していません。マルコフモデルはこのような現実的な構成を正確に評価できます。
診断範囲の低下 (DC=60%に低下)	1.03×10^6	≈1.58×10^7	d (附属書K) / d (モデル)	DCの低下はPFHを悪化させます。両手法ともPL dの範囲ですが、定量的な影響はマルコフモデルでより詳細に分析できます。

この表は、マルコフモデルの優位性を如実に示しています。「CCF対策強化」の行は、優れた設計努力がマルコフモデルでは報われるのに対し、簡略化手法では無視されることを示しています。「非対称チャネル」の行は、簡略化手法の硬直的な限界を明確に表しています。この表こそが、「なぜ私たちは、この新しい手法を学ぶ手間に価値があるのか？」という問いに対する、最も説得力のある答えなのです。

第6部：高度な考察と未来への備え

7.1 安全性を超えて：修復可能システムとアベイラビリティのモデリング

このブログでは、主に危険側故障の発生頻度（PFH）の解析に焦点を当ててきました。しかし、マルコフモデルの応用範囲はそれに留まりません。モデルに「修復」のプロセス、すなわち修復率 μ を持つ遷移を組み込むことで、修復可能なシステムの挙動を詳細に分析することが可能になります 。

修復を考慮したモデルを用いると、PFHに加えて以下のような、ビジネス上重要な信頼性指標を算出できます。

これは、マルコフモデリングという単一のスキルセットが、安全性と運用効率という、これまで別々に扱われがちだった二つの領域を橋渡しすることを示唆しています。安全設計の過程で構築されたモデルや収集されたデータは、プラントの稼働率を予測し、メンテナンス計画を最適化しようとしているチームにとって、直接的な価値を持ちます。これにより、組織内の「安全部門」と「信頼性・保全部門」の間の壁が取り払われ、設計、安全性、信頼性、運用コストを同時に最適化する、より統合されたアプローチへの道が開かれます。これは、組織全体の効率性を高める大きな機会となるでしょう。

7.2 実践的な課題：「状態空間の爆発」

マルコフ解析を適用する上で、避けて通れない実践的な課題が「状態空間の爆発」です 。これは、システムを構成するコンポーネントの数が増えるにつれて、システム全体として取りうる状態の数が指数関数的に増大する現象を指します。

例えば、それぞれが「正常」と「故障」の2状態を持つコンポーネントが10個あるだけで、システム全体の状態数は 2^10=1024 にもなります。20個なら100万を超えます。このように状態数が膨大になると、手作業でのモデル構築は不可能になり、コンピュータによる計算も膨大なリソースを要するようになります。

この課題のため、マルコフ解析は通常、システム全体を一度にモデル化するのではなく、SRP/CSを構成するサブシステム（入力、ロジック、出力など）単位で適用され、その結果が統合されることが一般的です。

状態空間爆発の課題に対応し、複雑なシステムのマルコフ解析を現実的に行うためには、専用のソフトウェアツールの活用が不可欠です。これらのツールは、状態遷移図のグラフィカルな構築、遷移率行列の自動生成、微分方程式系の数値解析、そしてPFHやアベイラビリティといった各種信頼性指標の計算を自動で行う機能を提供します。

自分でプログラムを作ってみた

難しい数式ばかりだと、少し疲れてしまいますよね。
そこで、理論を少しでも身近に感じていただけるよう、マルコフの微分方程式を基にした計算プログラムを作成してみました。

あくまで簡易的なものですので、計算結果は参考値としてご覧いただければ幸いです。

8.0 結論と私たちの業界への戦略的提言

本ブログ記事では、ISO/TR 13849-3の核心である、マルコフモデルに基づいたPFH計算手法について、その理論的背景から具体的な適用方法、そして実践的な意味合いに至るまでを詳細に解説してきました。

ISO/TR 13849-3は、これまでISO 13849-1の附属書Kの背後に隠されていたPFH計算の理論的根拠を明らかにし、機能安全評価の透明性、厳密性、そして柔軟性を大きく前進させる、画期的な文書です。この手法は、簡略化手法では扱えなかった非標準アーキテクチャや複雑なシステムの安全性を正確に評価することを可能にし、優れた設計努力を定量的に評価することで、より最適化された安全設計を促進します。

この新たな技術報告書の登場を踏まえ、機械安全に携わる専門家として、私たちは以下の戦略的アプローチを取ることが推奨されます。

1. 単純なSRP/CS（PL a～PL c）に対して:

ISO 13849-1の簡略化手法は、依然として有効かつ効率的なアプローチです。これらのリスクレベルでは、簡略化手法の保守性と簡便性が、厳密なモデル化の労力を上回る場合が多いため、引き続き活用することが推奨されます

2. 高信頼性SRP/CS（PL d～PL e）または非標準アーキテクチャに対して:

マルコフモデリングに関する社内専門知識を育成するか、外部の専門家と連携することを積極的に検討すべきです。これらのケースでは、安全性の主張を客観的かつ定量的に立証するためのベストプラクティスとして、マルコフ解析が事実上の標準となる可能性が高いです。これは、もはや選択肢ではなく、当然の責務（due diligence）となりつつあります。

3. 全ての専門家に対して:

たとえ日常業務でソフトウェアツールを使用するとしても、ISO/TR 13849-3に示される基本原理を理解することが極めて重要です。これにより、ツールの出力結果を鵜呑みにするのではなく、その背後にある仮定を批判的に評価し、得られた結果を正しく解釈する能力が養われます。ツールを「ブラックボックス」として扱わず、その意味を深く理解し、説明責任を果たすことこそが、プロフェッショナルとしての責務です。

結論として、ISO/TR 13849-3は、私たち機械安全の専門家にとって新たな挑戦であると同時に、より安全で革新的な機械を創造するための大きな機会を提供してくれます。この変化に積極的に対応し、先進的な信頼性評価手法を習得することが、今後の機械安全分野における競争優位性の源泉となることは間違いないでしょう。

---

ここまでお読みいただきまして、ありがとうございます。少々難しかったかもしれません。今後も、最新のトピックやリクエストがあればそれに応えていこうと思います。