【機械安全プロフェッショナル向け】ISO 13855:2024の徹底解説 | 動的分離距離 “S” の求め方と解説 | AGVやロボットの分離距離が変わる！ -2-

みなさん、こんにちは。こんばんは。

節分を過ぎ、少しずつですが春の足音が聞こえてきましたね。皆さん、いかがお過ごしでしょうか。

冬の寒さが厳しいと「春はまだかな」と待ち遠しく感じるものですが、「冬来たりなば春遠からじ」という言葉の通り、季節は確実に巡っています。最近では、日差しが少し柔らかくなったり、風の冷たさの中にもどこか優しさを感じたりと、小さな春の兆しを見つけるたびに心がほっこりします。

空を見上げると、曇り空の合間から青空が顔をのぞかせる瞬間も増えてきました。まるで雲の向こうにはいつも蒼天が待っているかのように、希望を感じさせてくれる景色です。

これからますます暖かくなり、花々が咲き乱れる季節がやってきます。梅や桜が咲く頃には、また一段と外に出るのが楽しみになることでしょう。皆さんもぜひ、季節の移ろいを感じながら、心地よい春をお迎えください。

さて、季節が移り変わるように、機械安全の世界にも大きな変化の波が訪れています。
長らく改訂作業が続いていた、機械安全における最も基的かつ重要な安全規格の一つである「安全距離」に関する国際規格、ISO 13855がついに改訂されました。

第3版となるISO 13855:2024、およびEN規格であるEN ISO 13855:2025の発行は、2010年版以来およそ15年ぶりの大改訂となります。

今回の記事は、以前ご紹介した静的分離距離に続く追加バージョンとしてお届けします。前回の記事では静的な環境における距離の考え方をお話ししましたが、今回は「動的分離距離」について深掘りしていきます。

---

この15年間で、製造現場の風景は劇的に変化しました。
かつては安全柵やガードの中に隔離されていた産業用ロボットが、柵の外に出て人と同じ空間を共有するようになりました。また、AGVと呼ばれる無人搬送車や、AMRといった自律走行搬送ロボットが工場内を走り回る姿も珍しくありません。

このような「機械も人も動く」という環境においては、従来の「固定された機械に人が近づく」という前提に基づいた計算式だけでは、安全を担保することが難しくなってきました。接触などの可能性が予見される場面が増えているからです。

今回の改訂における最大のトピックは、まさにこの新しい環境に対応するために新設された第6章の「動的分離距離」です。英語ではDynamic Separation Distanceと表記されます。これまでの静的なアプローチから動的なアプローチへの転換は、単なる計算式の変更にとどまりません。安全設計の思想そのもののアップデートを私たちに求めていると言えるでしょう。

本稿では、ある程度機械安全の知識をお持ちの方を対象に、このISO 13855:2025の核心部分について解説します。特に第6章の動的分離距離に特化し、その理論的背景から具体的な計算手法、そして実務への影響までを可能な限り詳細に紐解いていきます。

1. 静的アプローチから動的アプローチへ

1.1 用語の変化：「最短距離」から「分離距離」へ

まず最初に、規格のタイトルや基本的な用語の変化について触れておく必要があります。旧版（2010年版）では、計算によって求められる距離を「最短距離（Minimum Distance）」と呼んでいました。しかし、新規格ではこれが「分離距離（Separation Distance）」という用語に統一されています。

これは単なる言葉の綾ではありません。「最短」という言葉には「これ以上近づいてはいけない固定的な境界線」というニュアンスが含まれていました。一方で「分離（Separation）」という言葉は、人とハザード（危険源）を物理的・時間的に「引き離す」という機能的な意味合いが強くなっています。特に、今回導入されたSSC（速度・分離監視）のように、状況に応じて必要な距離が変化する動的な制御を扱う上では、「分離」という表現の方がより適切であると判断されたのです。

1.2 なぜ「動的」な考え方が必要だったのか

2010年版のISO 13855における基本式は、以下の通りでした。

$$S = (K \times T) + C$$

この式は、「危険源の位置は固定されており（例：プレス機の金型）、そこに人が移動して近づく」という静的危険源を前提としていました。

しかし、AGVやAMR、あるいは走行軸に乗ったロボットのように、危険源自体が移動する場合、相対的な接近速度は人の歩行速度 K だけでは決まりません。機械が人に向かってくる速度も考慮する必要があります。これまで、こうしたケースはISO/TS 15066（協働ロボット）などの個別規格で補完されてきましたが、B規格（基本安全規格）として体系化されてはいませんでした。

ISO 13855:2025では、これを「動的危険源（Dynamic Hazard）」と定義し（3.1.17）、危険源の発生源自体が移動する場合の距離計算を第6章で明確に規定しました。これにより、移動ロボットを含むあらゆる「動く機械」に対する安全距離の考え方が統一されたことになります。

1.3 新規格の構成と第6章の位置づけ

ISO 13855:2025ではページ数が大幅に増加し、構成も刷新されました。動的分離距離に関連する主要な構成は以下の通りです。

章番号	タイトル	概要
第4章	方法論	安全距離決定のフローチャートや基準面の考え方が整理されました。
第5章	分離距離	従来の静的な計算式（危険源が固定されている場合）がここに集約されています。
第6章	動的分離距離 (Dynamic Separation Distance)	【この記事】 危険源が移動する場合の計算式。未知の侵入方向と既知の侵入方向に分類されます。
第7章	侵入方向の考慮	検出ゾーンに対する直交・平行・角度付き侵入の定義。
Annex	附属書	システム応答時間の要素 (Annex F) や測定手法 (Annex B, D) などが詳細化されました。

2. 動的分離距離の基礎概念と全体応答時間 T

第6章の計算式に入る前に、すべての基礎となる「全体システム応答時間 T」の定義変更について理解しておく必要があります。動的な制御においては、わずかな時間の遅れが大きな距離の差となって現れるため、時間の定義がより厳密になっています。

2.1 全体システム応答時間 T の新定義

従来の T は、単純に「センサーが検知してから機械が止まるまでの時間」として扱われることが多かったですが、ISO 13855:2025では、制御システムのサンプリング周期を明確に組み込んだ以下の式が提示されています。

$$T = t_I + t_L + t_O + t_D + t_R + t_M + t_F + t_S$$

2.2 サンプリング間隔 t_S の重要性

ここで新たに明確化された t_S は、動的制御において極めて重要な意味を持ちます。

デジタル制御システムでは、入力を検知してから出力を行うまでに、必ず一定のサイクルタイム（スキャンタイム）が存在します。例えば、カメラで人を検知する場合、フレームレートが30fpsであれば、約33msの間隔でしか状況を更新できません。最悪の場合、検知の直後に新しいフレームが始まったとすると、次の検知までに最大で1サイクル分の遅れが生じます。

動的分離距離計算においては、この「検知の隙間」に機械と人がどれだけ接近するかを無視できません。上記式において t_S を加算することは、「検知が次のサンプリングの冒頭で発生したとしても安全を担保する」というワーストケースの設計思想を反映しています。

特に、後述する「既知の侵入方向（ベクトル演算）」を行う場合、この t_S には 0.1秒（100ms）以下 という厳しい制約が課されることになります。これについては第4章で詳しく解説します。

3. 未知の侵入方向に対する動的分離距離（6.2項）

第6章は大きく2つのセクションに分かれています。まずは、6.2項で扱われる「人の侵入方向が未知（Unknown）」の場合です。

3.1 想定されるシナリオ

これは、AGVやAMRがオープンスペースを走行しているような状況を想定してください。360度どこから人が飛び出してくるかわかりません。あるいは、搭載しているセーフティレーザスキャナが「物体の有無」だけを検知し、「物体の移動ベクトル（どちらに向かって動いているか）」までは特定できない場合もこれに該当します。

この場合、安全設計としては「人は最も危険な方向（正面衝突コース）から近づいてくる」と仮定して計算する必要があります。

3.2 基本計算式

未知の侵入方向に対する動的分離距離 S の計算式は以下の通りです。

$$S = (K \times T) + S_M + D_{DS} + Z$$

静的な計算式と比較して、新たに S_M という項が追加されていることがわかります。

3.3 S_M 危険源位置の変化量の計算詳細

S_M は、単なる「ブレーキ距離」ではありません。制御の遅れや、その間に機械が加速する可能性までを含んだ、非常に厳密な物理計算が求められます。

加速度と減速度が既知の場合

機械の加速度 a と減速度 d がわかっており、一定であると仮定できる場合、S_M は以下の式で算出されます。

$$S_M = v_0 \times T – \frac{d}{2} \times {t_M}^2 + \frac{a}{2} \times {t_{SRP/CS}}^2$$

この式の意味を分解してみましょう。

項	意味	解説
$$v_0 \times T$$	初速度での移動距離	検知した瞬間 t=0 の速度 v0 で、システム応答時間 T の間進み続けたと仮定した距離です。
$$\frac{d}{2} \times {t_M}^2$$	減速による短縮分	ブレーキが効いている時間 tM の間に、減速度 d によって短縮される距離を引きます。ブレーキ性能が良いほど、この項が大きくなり、SM は短くなります。
$$\frac{a}{2} \times {t_{SRP/CS}}^2$$	加速による増加分	【重要】 センサーが検知してから、実際にブレーキ指令が機械に届くまでの制御遅れ時間 tSRP/CS の間は、機械はまだ「加速中」である可能性があります。その分の移動距離を加算します。

多くの設計者は「検知したらすぐ減速する」と考えがちですが、この式は「制御信号が伝わるまでは加速し続けているかもしれない」という最悪のケースを想定しています。特にAGVなどの場合、加速中に検知することは十分にあり得ます。以下の「減速による短縮分」と「加速による増加分」の項の存在が、ISO 13855:2025の厳密さを象徴しています。

$$-\frac{d}{2} \times {t_M}^2+\frac{a}{2} \times {t_{SRP/CS}}^2$$

加速度 a が不明な場合

機械の加速度 a が正確にわからない場合、システムが測定した速度差などから推測するか、以下の簡略式を用います。

$$S_M = v_0 \times T – \frac{d}{2} \times {t_M}^2 + \frac{v_{max} – v_0}{2} \times t_{SRP/CS}$$

ここでは、現在の速度 v₀ から最大速度 v_max までの変化を考慮して加速分を見積もります。

無限の加速度を想定する場合

さらに保守的に、「機械は瞬時に最大速度まで加速するかもしれない」と想定する場合（あるいは加速度計算が困難な場合）は、以下の式を用います。

$$S_M = v_{max} \times T – \frac{d}{2} \times {t_M}^2$$

ここでは初速度 v₀ ではなく、機械の最大能力である v_max を用いて計算します。これにより、S_M は大きくなり、結果として必要な分離距離も長くなります。

減速度 d が不明な場合

もし、ブレーキ性能が保証されていない、あるいは減速度 d が未知である場合は、d=0 として計算しなければなりません。 つまり、ブレーキによる短縮分（マイナスの項）が消滅し、慣性で滑走し続ける前提での計算となります。これは非常に長い分離距離を要求することになるため、実務上は「減速度の明確化（および保証）」が必須となるでしょう。

4. 既知の侵入方向に対する動的分離距離 (6.3項)

次に、6.3項で扱われる「人の侵入方向が既知（Known）」の場合です。ここが、新規格における最も技術的に高度で、かつシステムインテグレーターにとって腕の見せ所となる部分です。

4.1 ベクトル演算による距離の最適化

高機能なセーフティカメラやAI画像処理技術を用いれば、単に「人がいる」だけでなく、「人がどちらに向かって動いているか」を検知できる場合があります。

• シナリオA： 人がAGVに向かって正面から走ってくる（相対速度＝最大）
• シナリオB： 人がAGVと同じ方向に逃げている、あるいは横切ろうとしている（相対速度＝小さい）

シナリオBの場合、未知の方向として計算すると過剰な安全距離をとることになり、AGVは頻繁に停止して生産性が低下します。6.3項では、ベクトル演算を用いてこの距離を最適化（短縮）することを認めています。

4.2 計算式と余弦定理

既知の方向に対する動的分離距離 S は以下の通りです。

$$S = S_A + D_{DS} + Z$$

ここで、S_A（動的アプローチにおける分離距離）は、以下の余弦定理を用いた式で求められます。

$$S_A = \sqrt{{S_M}^2 + {S_P}^2 – 2 S_M \times S_P \times \cos(\gamma)}$$

4.3 角度 γ の影響力

この式における cos(γ) が、計算結果に劇的な影響を与えます。

正面衝突コース　γ=180°

cos(180°)=-1 となり、式は以下になります。

$$\sqrt{S_M^2 + S_P^2 + 2 S_M S_P} = \sqrt{(S_M + S_P)^2} = S_M + S_P$$

これは、「機械の移動距離」と「人の移動距離」を単純に足し算する状態で、6.2項の「未知の方向」と同じ結果（最大距離）になります。

追従・離脱コース　γ=0°

cos(0°)=1 となり、式は以下になります。

$$\sqrt{(S_M – S_P)^2} = |S_M – S_P|$$

人が機械を追いかけている場合など、相対的な接近距離は非常に小さくなります。理論上、安全距離を大幅に短縮できます。

直交コース γ=90°

cos(90°)=0 となり、式は以下になります。

$$\sqrt{S_M^2 + S_P^2}$$

4.4 【重要】サンプリング間隔の制約 0.1秒ルール

このベクトル演算を使えば、生産性を維持しながら安全を確保できる「夢のような機能」に思えますが、規格は実務的な落とし穴を設けています。それが、第2章でも触れたサンプリング間隔の制約です。

ISO 13855:2025では、6.3項の計算を適用する条件として以下を規定しています。

危険源の移動角度 αと人の接近角度 β を測定する間のサンプリング間隔 t_S は、0.1秒 (100ms) を超えてはならない

もし、使用している検知システム（カメラやLiDARのデータ処理）のサイクルタイムが 0.1秒を超えてしまう場合、人の動きの変化（急な方向転換など）を見落とすリスクが高すぎると判断されます。その場合、6.3項の計算式は使用できず、強制的に6.2項（未知の方向）の式を使用しなければなりません。

「AIカメラで人の向きを検知して安全距離を可変にしよう」と企画しても、画像処理の遅延や通信遅延でシステム全体の更新周期が100msを超えていれば、規格適合上はその機能を使って距離を短縮することはできません。これはシステム選定におけるクリティカルな要件となります。

第5章：SSC 速度・分離監視の実装要件

動的分離距離の概念は、SSC (Speed and Separation Control) という安全機能の実装と密接に関わっています。ISO/TS 15066で協働ロボット向けに定義されていた SSC が、今回のISO 13855改訂で一般機械にも正式に適用されることになりました。

5.1 SSC の定義と役割

SSC とは、検出された人体の位置に応じて機械の速度や軌道を変化させ、適切な分離距離を維持することでリスク低減を達成する安全機能です。この分離距離は、人体や機械の速度および移動方向、保護装置の検出能力、制御システムの応答時間といった複数のパラメータによって決定されます。

Speed and separation control, SSC

SSC とは、その安全機能が、機械またはその部品の速度および／または軌道を、人体部位の検出位置に対して変更することにより、分離距離を維持することで意図されたリスク低減を達成するもの

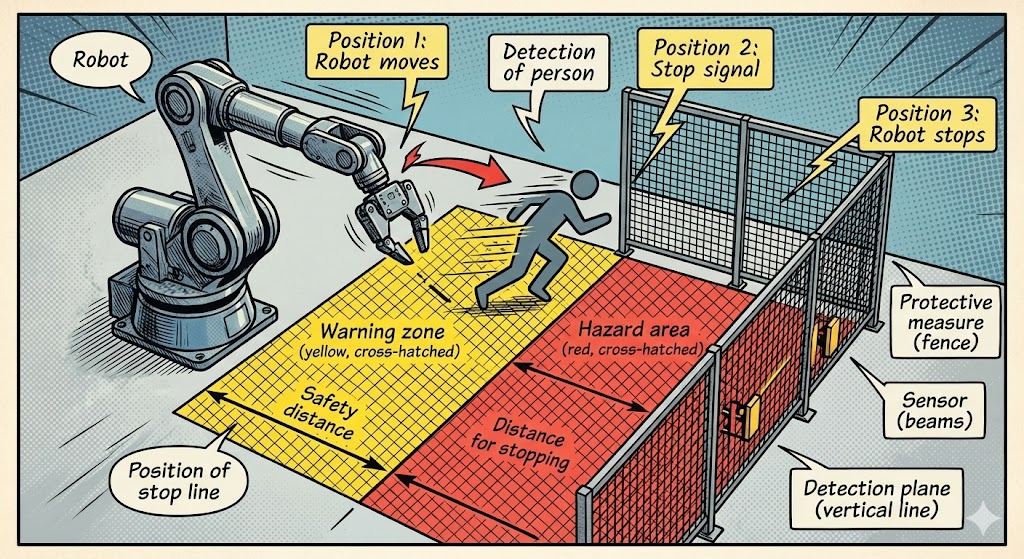
つまり、従来の「エリアに入ったら停止（Stop）」という0か1かの制御ではなく、以下のような連続的な制御を行います。

5.2 新規格における SSC の実装要件

第6章の計算式を SSC に適用する場合、以下の要件を満たす必要があります。

6. 接近方向の幾何学モデルの詳細解説

前章で解説したベクトル演算（6.3項）の前提として、ISO 13855:2025の規格書内では「Figure 5 接近方向」という図が示されています。この図は、動的分離距離を計算する際の人と機械の空間的な位置関係を厳密に定義する重要なモデルです。

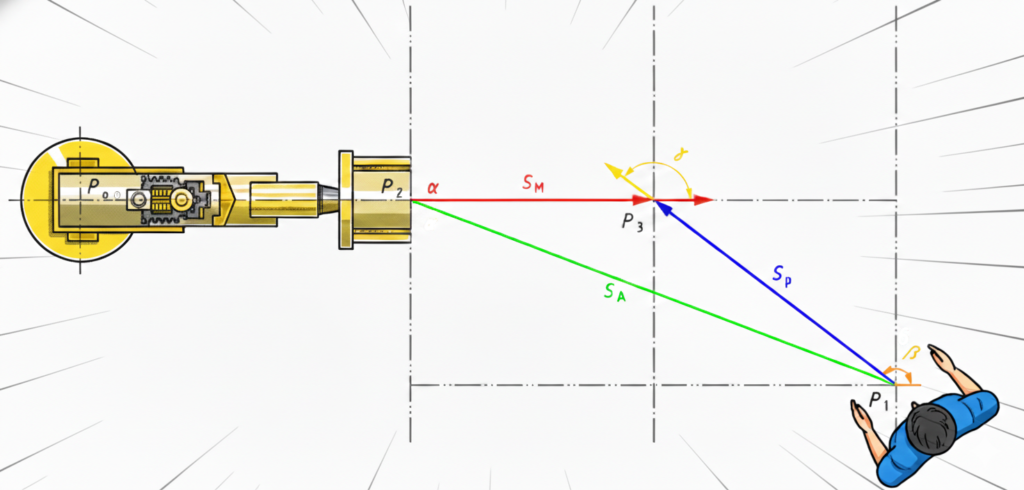
ここでは、Figure 5で定義されている各パラメータの意味を詳しく紐解いていきましょう。

6.1 時間と座標の定義

図中では、危険な事象の推移を以下の2つの「時間」と、それに伴う「位置」で定義しています。

T₀ トリガー時間

センサー等の保護装置が人の侵入を検知し、安全機能がトリガーされた瞬間です。

T₁ リスク低減完了時間

ブレーキ等が作動し、機械が完全に停止（または意図したリスク低減が完了）した瞬間です。全体システム応答時間 T は以下の式になります。

$$T = T_1 – T_0$$

6.2 距離ベクトルの定義

このモデルでは、2つの重要な移動距離がベクトルとして扱われます。

S_M 危険源の移動距離

P₂ から P₃ へ至る機械の移動距離です。これは初速度 v₀ 、減速度 d、および応答時間 T を用いて計算されます（第3章で解説した式と同様です）。

$$S = (K \times T) + S_M + D_{DS} + Z$$

S_P 人の移動距離

時間 T₀ から T₁ の間に、人が一定の最大速度で移動し続けたと仮定した距離です。

$$S_P = K \times T$$

6.3 角度と γ の算出

ベクトル演算の要となるのが、それぞれの進行方向を示す角度です。基準となるX軸に対する角度として以下が定義されています。

ISO 13855:2024 の注記によれば、このγは固定値ではなく、機械の制御システムが危険源の移動方向を常時センシングし、さらに適切な保護装置（高性能なセーフティスキャナやAIカメラなど）が人の接近方向を検出することによって、システム内部で決定（計算）されるものとされています。

この Figure 5 の幾何学モデルによって導き出された S_M、S_P、および γを、第4章で紹介した余弦定理の式

$$S_A = \sqrt{{S_M}^2 + {S_P}^2 – 2 S_M \times S_P \times \cos(\gamma)}$$

に当てはめることで、初めて「動的アプローチにおける分離距離 S_A」が算出される仕組みになっています。

---

ここまでお読みいただきありがとうございました。

ISO 13855:2025は、機械安全の世界に「動的（Dynamic）」という概念を正式に持ち込みました。数式が増え、一見すると難解になったように感じるかもしれませんが、その背景にあるのは「機械の動きを正確に物理モデル化し、過不足のない最適な安全距離を導き出す」という合理的な思想です。

特に、AGVや協働ロボットの普及により、「止める安全」から「動きながら守る安全」へのニーズは高まる一方です。6.3項のベクトル演算などは、まさにそのための強力なツールとなるでしょう。

この新しい規格を正しく理解し、設計に取り入れることで、安全性と生産性を高い次元で両立させることが可能になります。

今回の記事が、皆様の安全設計の一助となれば幸いです。